이진 트리(Binary Tree)를 탐색하는 방법에는 크게 다음의 4가지가 있다.

• 전위순회(Preorder Traversal)
• 중위순회(Inorder Traversal)
• 후위순회(Postorder Traversal)
• 레벨순회(Levelorder Traversal) 또는 BFS(Breadth-First Search; 너비 우선 탐색)

레벨순회(;BFS)를 제외한 나머지 순회방식은 DFS(Depth-First Search; 깊이 우선 탐색)으로 분류할 수 있다.

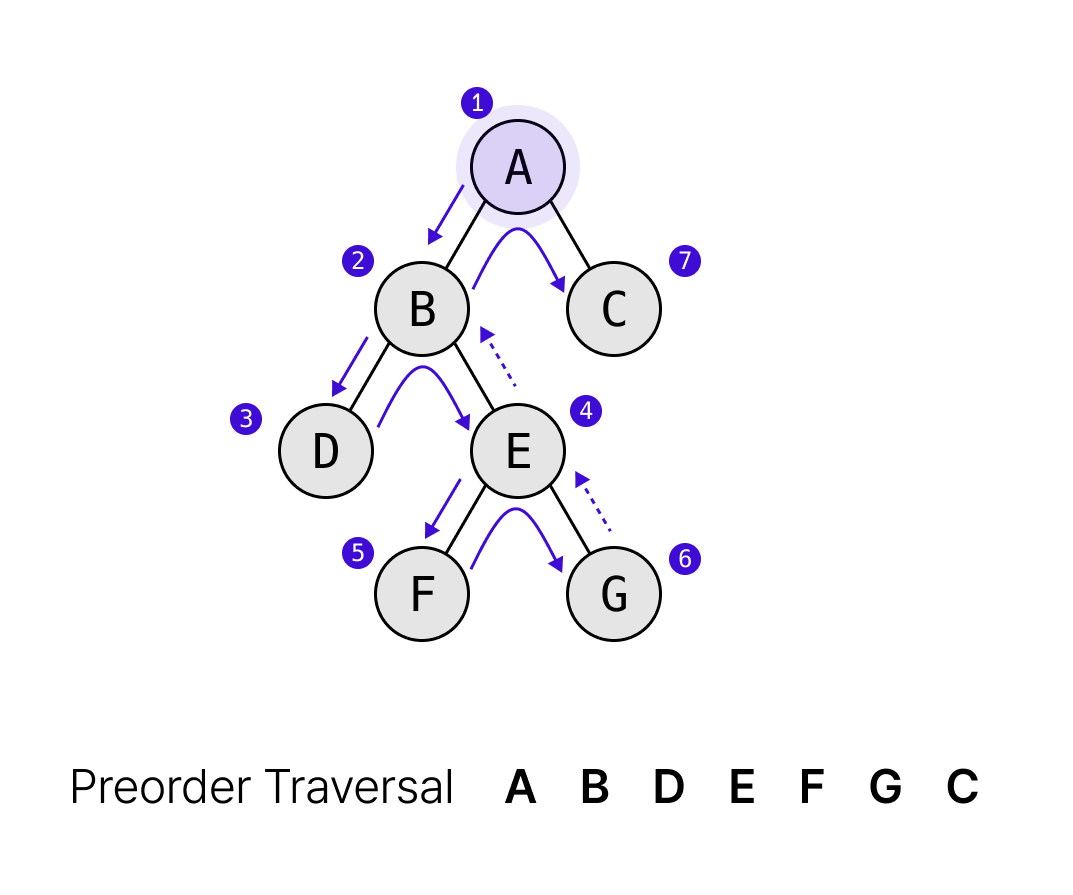
전위순회(preorder traversal)

전위순회는 루트 노드를 먼저 탐색하고, 자식 노드를 탐색하는 방식이다.

void preorder(Node* root) {
    if (root == nullptr) return;
    cout << root->data << " ";
    preorder(root->left);
    preorder(root->right);
}

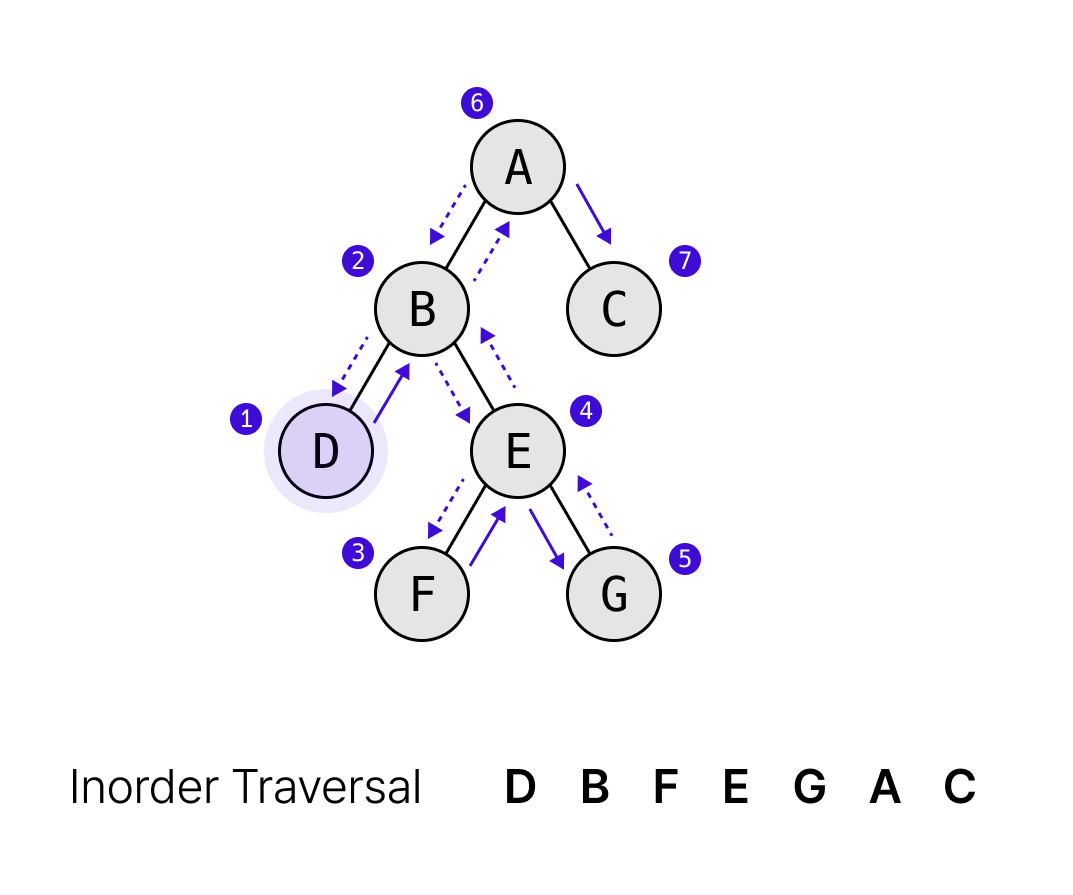
중위순회(inorder traversal)

중위순회는 왼쪽 자식 노드를 탐색하고, 루트 노드를 탐색하고, 오른쪽 자식 노드를 탐색하는 방식이다.

void inorder(Node* root) {
    if (root == nullptr) return;
    inorder(root->left);
    cout << root->data << " ";
    inorder(root->right);
}

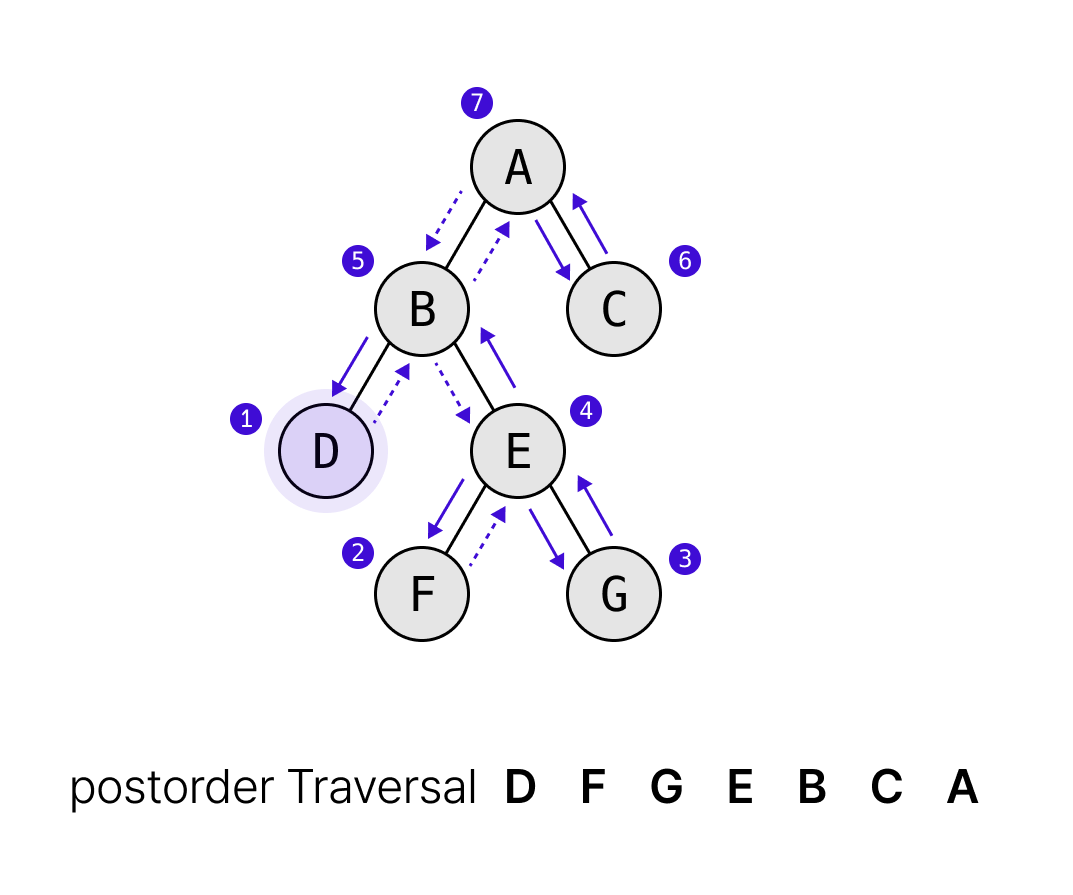
후위순회(postorder traversal)

후위순회는 왼쪽 자식 노드를 탐색하고, 오른쪽 자식 노드를 탐색하고, 루트 노드를 탐색하는 방식이다.

void postorder(Node* root) {
    if (root == nullptr) return;
    postorder(root->left);
    postorder(root->right);
    cout << root->data << " ";
}

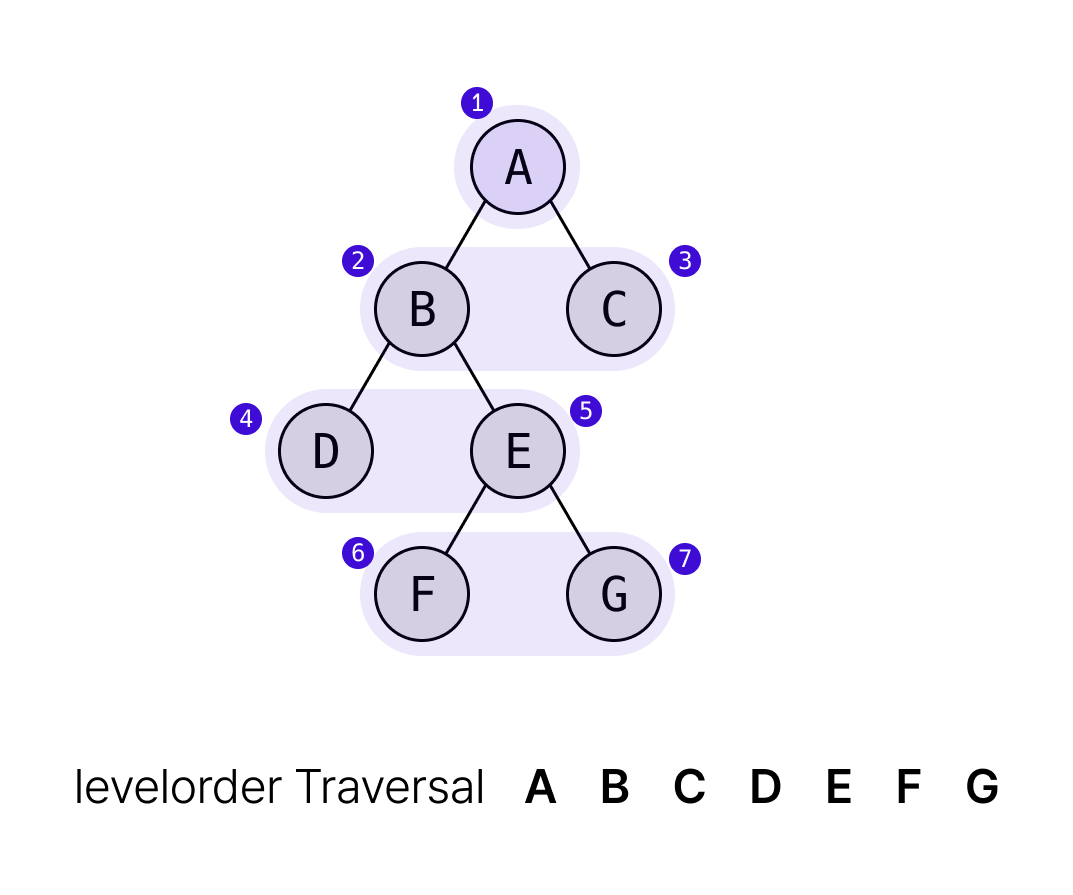
레벨순회(levelorder traversal; BFS)

레벨순회는 루트 노드를 먼저 탐색하고, 그 다음 레벨의 노드를 탐색하는 방식이다. queue를 하나 선언해두고, 루트 노드를 넣어준 다음, queue에 넣어준 노드를 하나씩 탐색하면서 자식 노드를 queue에 넣는다. queue가 비어있을 때까지 반복한다.

void levelorder(Node* root) {
    if (root == nullptr) return;
    queue<Node*> q;
    q.enqueue(root);
    while (!q.isEmpty()) {
        Node* cur = q.dequeue()
        cout << cur->data << " ";
        if (cur->left != nullptr) q.enqueue(cur->left);
        if (cur->right != nullptr) q.enqueue(cur->right);
    }
}

레벨순회의 작동 방식

다른 순회 방식은 재귀로 쉽게 구현이 가능하지만, 레벨 순회(;BFS)는 재귀가 아닌 다른 방식으로 구현해야 한다. 일반적으로 Queue를 사용하는데, 예시를 보며 작동 방식을 익혀보자.

A를 루트로 하는 트리가 있으면, A를 queue에 집어 넣는다.

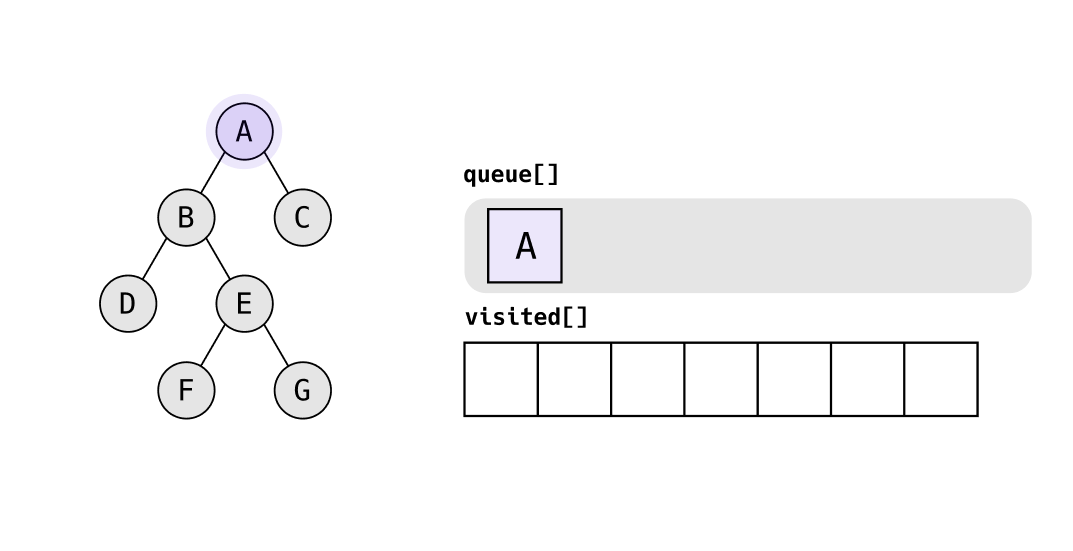
queue의 가장 앞에 있는 A를 탐색하고, A의 자식 노드 B, C를 queue에 집어 넣는다.

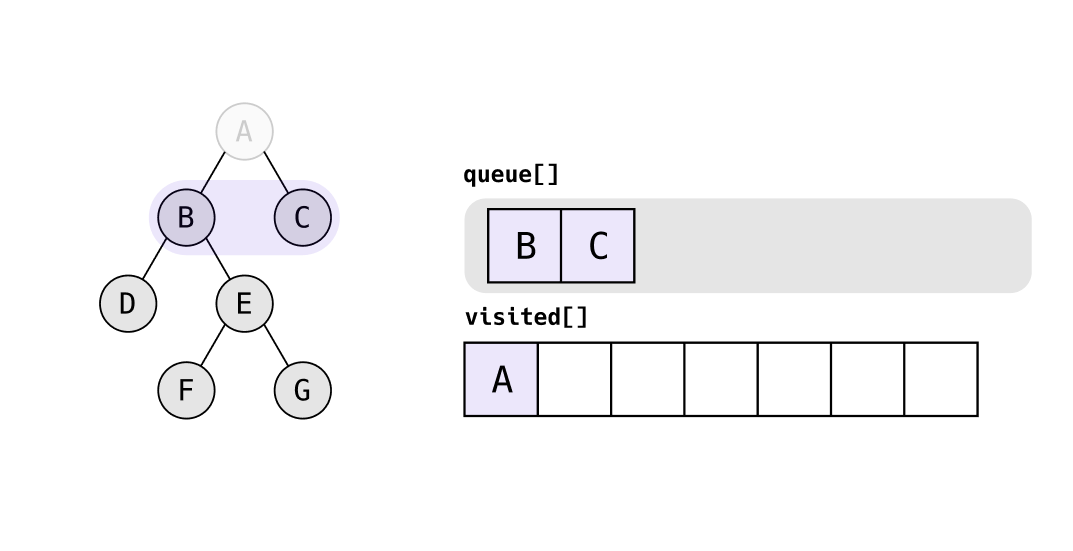
queue의 가장 앞에 있는 B를 탐색하고, B의 자식 노드 D, E를 queue에 집어 넣는다.

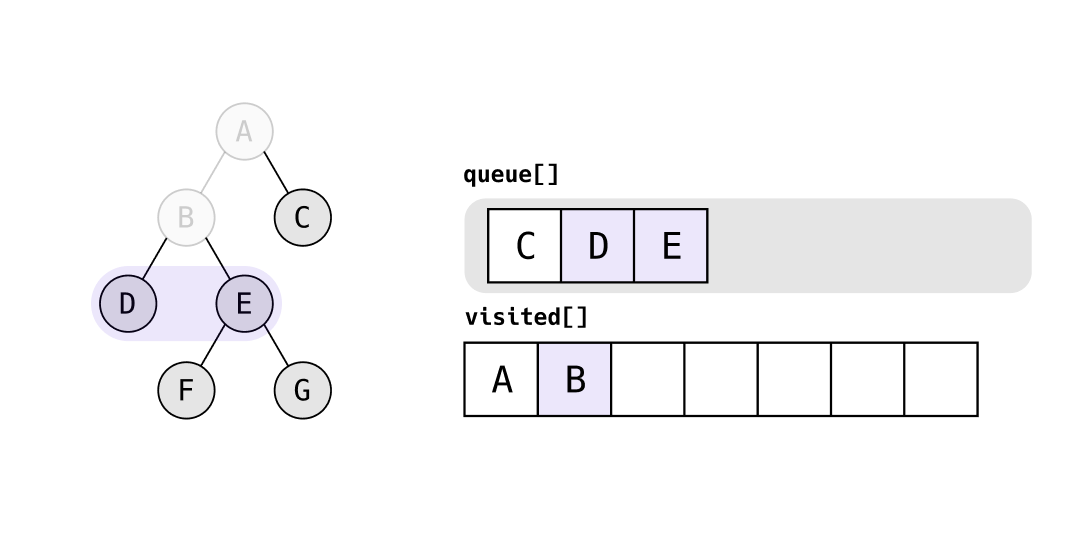
queue의 가장 앞에 있는 C를 탐색하고, C는 자식 노드가 없으므로 다음으로 넘어간다.

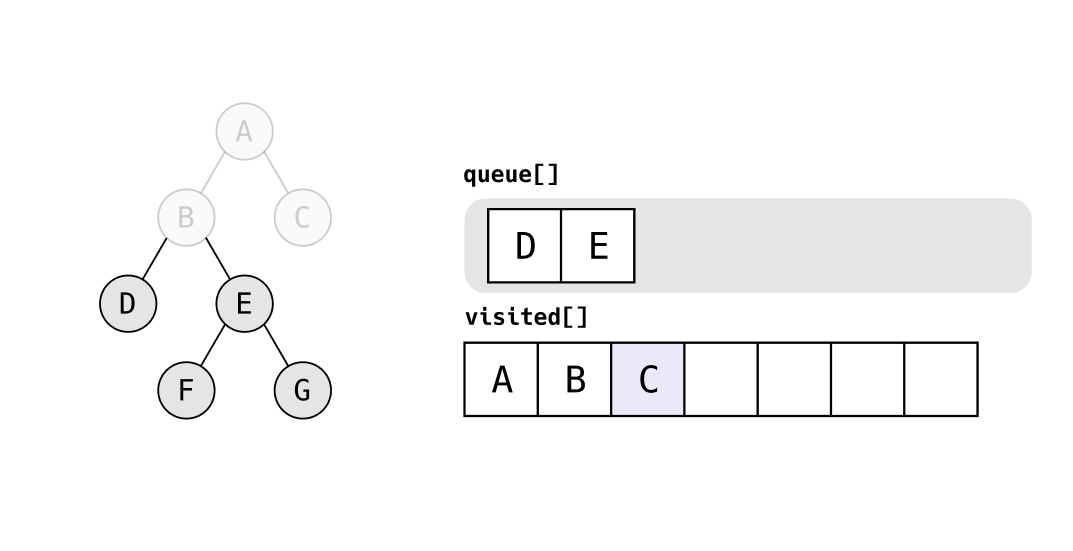
queue의 가장 앞에 있는 D를 탐색하고, D는 자식 노드가 없으므로 다음으로 넘어간다.

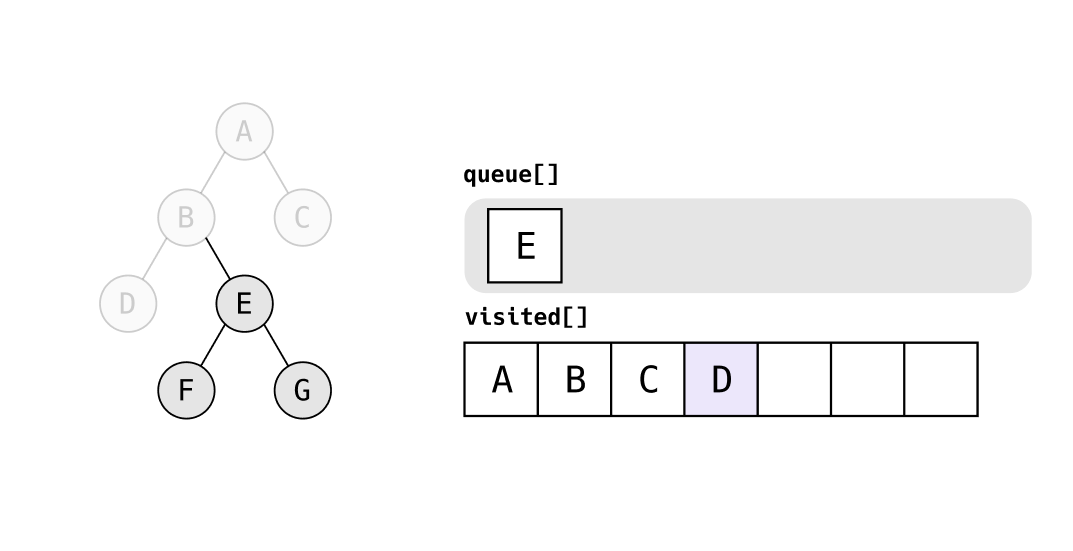
queue의 가장 앞에 있는 E를 탐색하고, E의 자식 노드 F, G를 queue에 집어 넣는다.

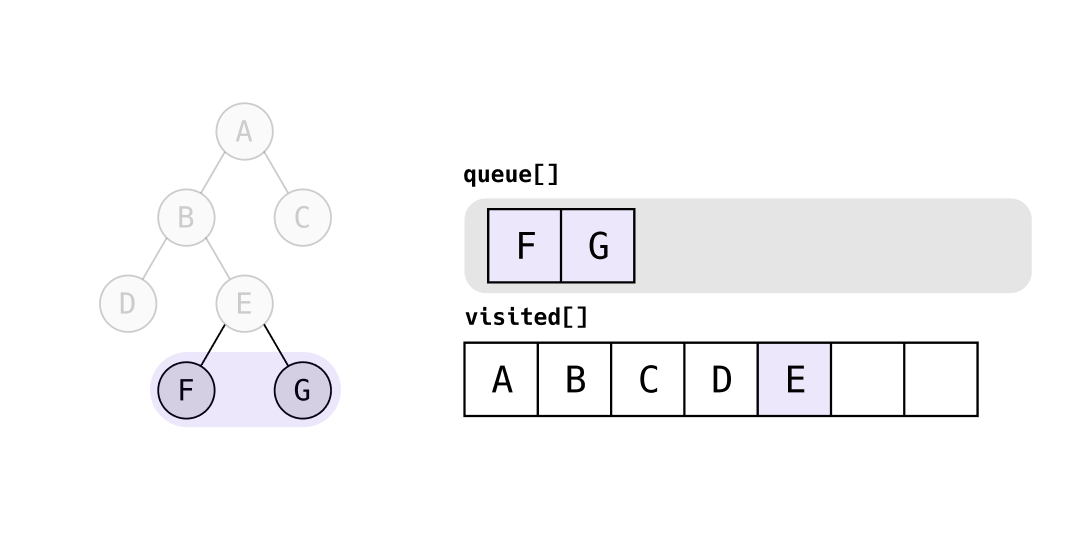
queue의 가장 앞에 있는 F를 탐색하고, F는 자식 노드가 없으므로 다음으로 넘어간다.

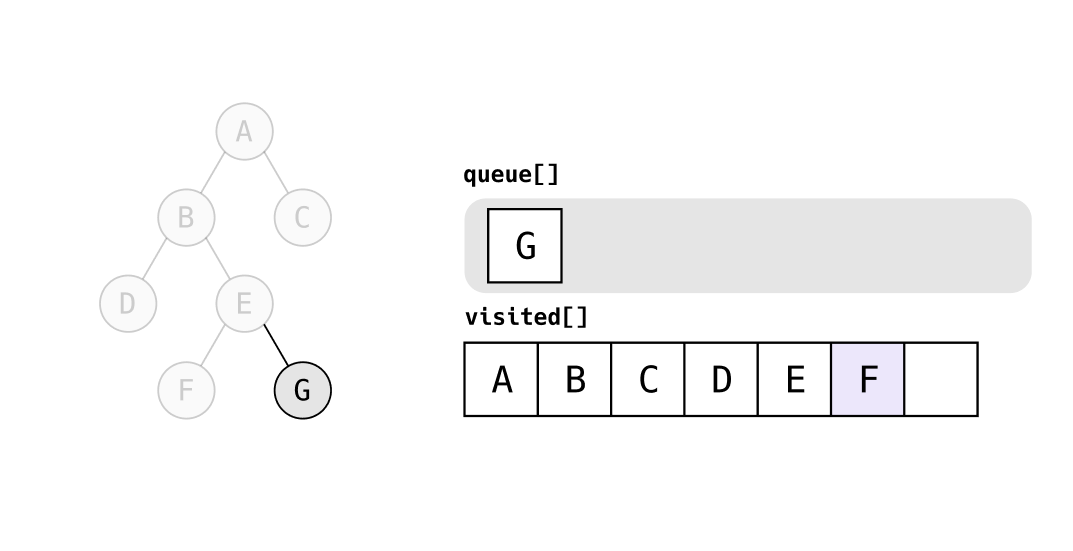
queue의 가장 앞에 있는 G를 탐색하고, G는 자식 노드가 없으므로 다음으로 넘어간다.

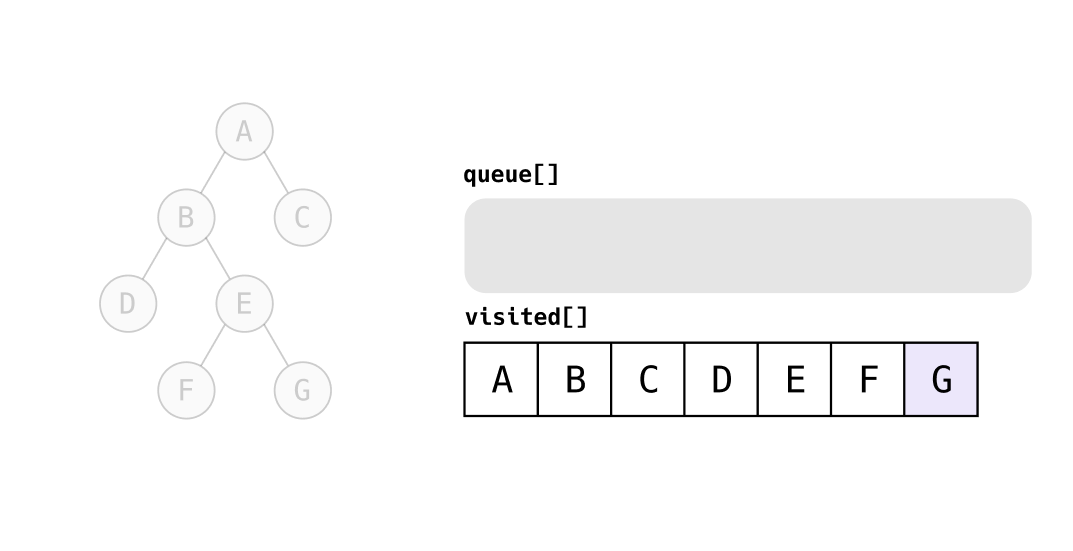
queue가 비었으므로 탐색을 종료한다.

이렇게 탐색을 완료하면 A, B, C, D, E, F, G 순으로 방문하게 된다.